对角线遍历

发表于 分类于 阅读次数： 本文字数： 642 阅读时长 ≈ 2 分钟

  1. 题目描述：

    给你一个大小为 m x n 的矩阵 mat ，请以对角线遍历的顺序，用一个数组返回这个矩阵中的所有元素。

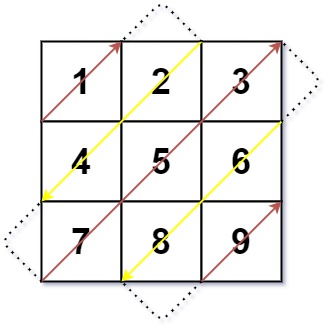
    输入：mat = [[1,2,3],[4,5,6],[7,8,9]]
    输出：[1,2,4,7,5,3,6,8,9]
    示例 2：

    输入：mat = [[1,2],[3,4]]
    输出：[1,2,3,4]

  2. 力扣官方题解

力扣官方题解更好理解一点。

  1. ChatGPT 题解：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function diagonalTraverse(mat) {
  // 行
  const m = mat.length;
  // 列
  const n = mat[0].length;
  // 初始化一个空数组 result，用于存储遍历后的结果
  const result = [];
  // 矩阵的对角线个数为 m + n - 1
  for (let i = 0; i < m + n - 1; i++) {
    const rowStart = Math.max(0, i - n + 1);
    const rowEnd = Math.min(i, m - 1);
    if (i % 2 === 0) {
      // 当 i 为偶数时，从下往上遍历，即 r 从 rowEnd 开始到 rowStart，对应的 c 为 i - r
      for (let j = rowEnd; j >= rowStart; j--) {
        result.push(mat[j][i - j]);
      }
    } else {
      // 当 i 为奇数时，从上往下遍历，即 r 从 rowStart 开始到 rowEnd，对应的 c 为 i - r
      for (let j = rowStart; j <= rowEnd; j++) {
        result.push(mat[j][i - j]);
      }
    }
  }

  return result;
}

解题思路：

初始化一个空数组 result，用于存储遍历后的结果。
外层循环遍历的次数为 m + n - 1，因为矩阵的对角线个数为 m + n - 1。
内层循环用于遍历当前对角线上的元素。
下面详细解释内层循环的处理过程：

对于每一条对角线，我们可以通过 i 的取值来确定 j 的范围，其中 i 代表当前对角线的索引，从 0 开始到 m + n - 2。
假设当前对角线上的元素为 (r, c)，其中 r 为行索引，c 为列索引，根据对角线的特点，有 r + c = i。
我们要在 r 的合理范围内遍历，因此 r 的范围为 Math.max(0, i - n + 1) 到 Math.min(i, m - 1)。当 i < n 时，r 的范围是从 0 开始到 i；当 i >= n 时，r 的范围是从 i - n + 1 开始到 m - 1。
根据 r 的取值，我们可以求出对应的 c，即 c = i - r。
接下来，根据 i 的奇偶性来决定遍历的方向：

当 i 为偶数时，从下往上遍历，即 r 从 rowEnd 开始到 rowStart，对应的 c 为 i - r。
当 i 为奇数时，从上往下遍历，即 r 从 rowStart 开始到 rowEnd，对应的 c 为 i - r。
根据上述规则，我们可以在内层循环中遍历当前对角线上的所有元素，并将其添加到结果数组 result 中。

最后，返回结果数组 result 即可得到按对角线遍历的顺序返回矩阵 mat 中的所有元素。