《深入浅出数据分析》读书笔记

发表于 更新于 分类于 阅读次数： 本文字数： 1.5k 阅读时长 ≈ 5 分钟

学习《深入浅出数据分析》，为了加深记忆，边读边做笔记。如有侵权，立即删除。

数据分析引言：分解数据

数据分析就是仔细推敲证据

所有优秀的分析师，无论专长及目标如何，都会在工作过程中按顺序执行下面这个固定基本流程，同时通过经验数据来仔细推敲各种问题。
数据分析的基本流程

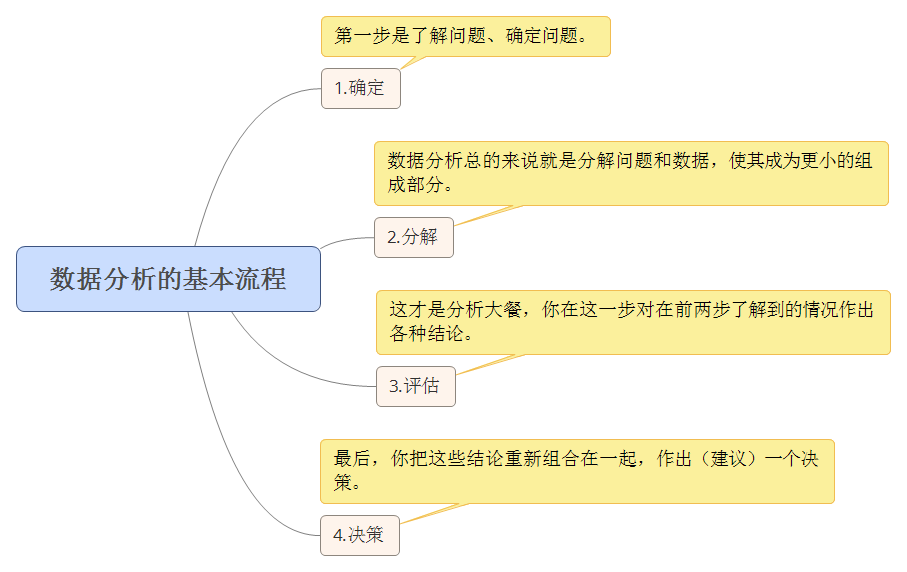
确定问题

未明确确定自己的问题或目标就进行数据分析就如同未定下目的地就上路旅行一样。

客户将帮助你确定问题，多向客户问问题。不断地问“是多少”，使你的各种目标和确信观点得到量化。

把问题和数据分解为更小的组块

将大问题划分为小问题
你需要将问题划分为可管理、可解决的组块。你面对的问题常常含糊不清，例如：
我们如何提高销量

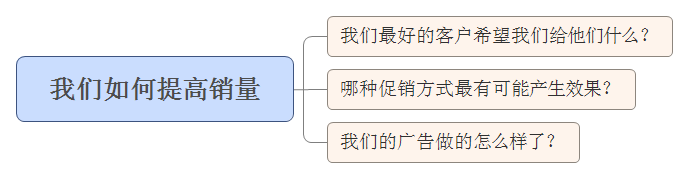
将数据分解为更小的组块
如果你拿到的是汇总情况，你就会想知道哪些因子对你至关重要。如果你拿到的是原始数据表，你就会想对这些因子进行汇总，让数据更有用。

实验：检验你的理论

务必使用比较法

统计与分析最基本的原理之一就是比较法，它指出，数据只有通过相互比较才会有意义。

最优化：寻找最大值

借助目标函数发现目标

目标函数：
$$c_1x_1 + c_2x_2 = P$$
其中：

  • 每个$c$ 表示一个约束条件
  • 每个$x$ 表示一个决策变量
  • $P$ 是你的目标，即期望的最大化对象

数据图形化：图形让你更精明

使用散点图探索原因

散点图是探索性数据分析的奇妙工具，统计学家用这个术语描述在一组数据中寻找一些假设条件进行测试的活动。
分析师喜欢用散点图发现因果关系，即一个变量影响另一个变量的关系。通常用散点图的$X$轴代表自变量（我们假想为原因的变量），用$Y$轴代表应变量（我们假想为结果的变量）。

假设检验：假设并非如此

变量之间可以正相关，也可以负相关

观察数据变量有一个好办法，问一问“这边变量是正相关还是负相关”，若一种变量增大意味着另一种变量也增大，则为正相关；若一种变量增大意味着另一种变量减小，则为负相关。

假设检验的核心是证伪

请勿试图选出最合理的假设，只需剔除无法证实的假设——这就是假设检验的基础：证伪。
选出看上去最可信的第一个假设的做法称为满意法。满意法的严重问题是，当人们在未对其他假设进行透彻分析的情况下选取某种假设时，往往会坚持这个假设，即使反面证据堆积如山，也往往视而不见。证伪法则让人们对各种假设感觉更敏锐，从而防止掉入认知陷阱。
进行假设检验时，要使用证伪法，回避满意法。

主观概率：信念数字化

主观概率体现专家信念

如果用一个数字形式的概率来表示自己对某事的确认程度，利用的就是主观概率。
主观概率是根据规律进行分析的巧妙方法，尤其是在预测孤立事件却缺乏从前在相同条件下发生过的事件的可靠数据的情况下。

直方图：数字的形状

将数据加载到R程序

1
source("http://www.headfirstlabs.com/books/hfda/hfda.R")

查看下载内容中的Employees数据框架，输入employees并回车。
在R中输入下面这条指令，生成直方图：

1
hist(employees$received,breaks = 50)

查看指定数据范围的标准偏差和汇总统计值

1
2
sd(employees$received)
summary(employees$received)

针对不同的数据分组计算直方图：

1
2
3
4
5
6
hist(employees$received[employees$year==2007],breaks = 50)
hist(employees$received[employees$year==2008],breaks = 50)
hist(employees$received[employees$gender=="F"],breaks = 50)
hist(employees$received[employees$gender=="M"],breaks = 50)
hist(employees$received[employees$negotiated==FALSE],breaks = 50)
hist(employees$received[employees$negotiated==TRUE],breaks = 50)

回归：预测

在R中运行这些指令，生成一张散点图，体现出要求加薪和实际加薪的情况。

1
2
3
employees <- read.csv("http://www.headfirstlabs.com/books/hfda/hfda_ch10_employees.csv",header=TRUE)
head(employees,n=30)
plot(employees$requested[employees$negotiated==TRUE],employees$received[employees$negotiated==TRUE])

使用R计算加薪数据的相关系数$r$。

1
cor(employees$requested[employees$negotiated==TRUE],employees$received[employees$negotiated==TRUE])

使用R创建自己的线性回归方程。

1
2
myLm <- lm(received[negotiated==TRUE]~requested[negotiated==TRUE],data=employees)
myLm$coefficients

合理误差

机会误差=实际结果与模型预测结果之间的偏差

实际结果与预测结果之间的偏差叫做机会误差。在统计学中，机会误差又称为残差，对残差的分析是优秀的统计模型的核心。

用均方根误差定量表示残差分布

使用R计算均方根误差：

1
2
3
4
5
6
7
8
# 加载最新数据
employees <- read.csv("http://www.headfirstlabs.com/books/hfda/hfda_ch10_employees.csv",header=TRUE)
# 线性模型对象
myLm <- lm(received[negotiated==TRUE]~requested[negotiated==TRUE],data=employees)
# R对模型的汇总
summary(myLm)
# 查看均方根误差
summary(myLm)$sigma

整理数据

整理数据的一般步骤

1.保存原始数据。
2.直观显示最终数据集。
3.识别数据中重复出现的模式。
4.整理和重新构建。
5.使用经过处理的数据。

完！

参考文档：
如何用excel求解器solver求出最优化解