《爱上统计学》读书笔记
学习《爱上统计学》,为了加深记忆,边读边做笔记。如有侵权,立即删除。
计算和理解平均数
描述统计(descriptive statistics)
描述统计常用于整理、描述所收集数据的特征。如描述大学最流行的的专业是什么。
推论统计(inferential statistics)
推论统计通常是(但并非总是)数据收集和汇总的下一步。推论统计常利用较小群体的数据来推论可能的较大群体的特征。
计算和理解平均数
平均数也叫做几种趋势量数(measures 偶发 central tendency),一般有三种形式:均值、中位数和众数。参看Wiki 百科。
计算均值
均值(mean)是计算平均数最常用的形式。均值很简单,就是数据组中所有数值的总和除以该组数值的个数。均值计算公式如下: $$ \overline{X} = \frac{\sum{X}}{X} $$ 其中
- 上带横线的字母X (读做“X bar”)是数据组的平均数或均值。
- ∑ 或希腊字母西格玛是连加符号,也就是将其后的所有数值都加起来。
- X 是数据组中每个具体的数值。
- 最后,n 是从中计算均值的样本的规模。
均值对极值很敏感。
计算中位数
中位数(median)被定义为一系列数据的中点。计算中位数的步骤:
- 以从大到小或者从小到大的顺序列出数值。
- 找到位于中间位置的数值。那就是中位数。
如果数值个数是偶数,中位数就是中间两个数值的平均是。中位数对极值不敏感。
均值是一系列数值的中间点,而中位数是一系列个体的中间点。
计算众数
众数(mode)就是出现次数最多的数值。
理解变异性
变异性(也叫做散布或离散度)可被看作是对不同数值之间的差异性的测量。如果把变异性看作是每个数值和特定值的差异程度可能更精确(而且也许更容易)。那么你认为哪一个“数值”可能被作为那个“特定值”呢?通常情况下这个“特定值”就是均值——很正确。因此,变异性成为测量数据组中每一个数值与均值的变异性的量数。
计算极差
极差是对变异性最笼统的测量。极差可让你了解数值之间彼此差异的程度。极差(range)是通过数据分布中的最大值减去最小值来计算。其计算公式: r = h − l 其中
- r 是极差
- h 是数据集中的最大值
- l 是数据集中的最小值
以下面的数据组(以降序的形式排列)为例:98,86,77,56,48。在这个案例中,98-48=50。极差是 50。
注意:实际上极差有两种类型。一种是不包含极差,也就是我们上面定义的。第二种是包含极差,就是最大值减去最小值再加 1(h − l + 1)。
计算标准差
标准差(standard deviation,缩写为s或SD)表示一个数据组中变异性的平均数量。实际的含义是与均值的平均距离。标准差越大,每一个数据点与数据分布的均值的平均距离越大。计算标准差的公式: $$s = \sqrt{\frac{\sum{(X - \overline{X})^2}}{n - 1}}$$ 其中
- s 是标准差
- ∑ 是西格玛,表示将其后所有数值累加求和
- X 是具体的数值
- $\overline{X}$ 是所有数值的均值
- $ n $ 是样本规模
为什么使用n − 1,而不是n
答案是s(标准差)是总体标准差的估计值,但是只有我们用 n 减去 1 的情况下才是无偏估计。我们把分母减去 1 会使得标准差大于实际的大小。为什么我们要这样做?因为好的科学家一般都是保守的。保守的含义是,如果我们不得不出错,我们出错也是由于过高估计了总体的标准差。除以较小的分母可让我们做到这一点。
注意:
- 标准差越大,数值分布越广,则数值之间的相互差异越大。
- 和均值一样,标准差对极值很敏感。当你计算样本的标准差时,若数据中存在极值,你就要在数据报告中注明这一点。
- 如果s = 0,数据组中就绝对没有变异性,而且在数值上完全一致。这种情况很少发生。
计算方差
方差(variance),就是标准差的平方。公式: $$s^2 = \frac{\sum{(X - \overline{X})^2}}{n - 1}$$
计算相关系数
相关系数到底是什么
相关系数(correlation coefficient)是反映两个变量之间线性关系的数值性指标。这个描述统计值的值域范围是-1 到 1.两个变量的相关有时也叫做二元相关。
相关反映变量间关系的动态性质。如果变量变化方向相同,相关是直接相关或正相关(direct correlation 或 positive correlation).如果变量变化方向相反,相关是间接相关或负相关(indirect correlation 或 negative correlation)。
相关系数的绝对值反映相关的强度。
皮尔逊积矩相关系数用小写字母r表示,r的下标表示相关的两个变量。例如:rXY 是变量X和变量Y之间的相关系数。
计算简单相关系数
变量X和变量Y之间的简单皮尔逊积矩相关系数的计算公式: $$r_{XY} = \frac{n\sum{XY} - \sum{X}\sum{Y}}{\sqrt{\left[n\sum{X^2} - (\sum{X})^2 \right]\left[n\sum{Y^2} - (\sum{Y})^2 \right]}}$$ 其中:
- rXY是X与Y之间的相关系数
- n是样本规模
- X是变量X的具体数值
- Y是变量Y的具体数值
- XY是每一个X值与相应的Y值的乘积
- X2是X值的平方
- Y2是Y值的平方
检验你的问题
零假设
我们已经从总体中选择了一个样本来检验我们的研究假设,我们首先要建立零假设(null hypothesis)。零假设宣称两个或多个事物之间是等同的或没有关系的。
零假设的目的
零假设既是研究起点也是测量实际的研究结果的基准。
首先,零假设是研究的起点,因为在没有其他信息的情况下零假设就被看作可接受的真实状态。换句话说,直到你能证明存在差异,否则你只能假定没有差异。而无差异或无关的陈述正是零假设的所有内容。
零假设的第二个目的是提供与观察到的结果进行比较的基准,进而分析是否是由于其他因素引起这些差异。零假设有助于定义观察到的群体间的差异范围是由偶然性引起(这是零假设的论点)还是由偶然性之外的因素引起。
研究假设
研究假设(research hypothesis)是变量间有关系的明确陈述。
如果研究假设假定不等价关系没有方向(例如“不同于”),假设就是无方向研究假设。如果研究假设假定不等价关系有方向(例如“多于”或“少于”),这个研究假设就是有方向研究假设。
无方向研究假设
无方向研究假设(nondirectional research hypothesis)反映群体间的差异,但是差异的方向是不确定的。可以用下面的式子表示:$$H_i:\overline{X}\_9 \neq \overline{X}\_{12}$$ 其中
- Hi 表示第一个(可能有几个)研究假设的符号
- $\overline{X}\_9$ 表示 12 年级学生样本的平均记忆成绩
- $\overline{X}_{12}$ 表示 9 年级学生样本的平均记忆成绩
- ≠ 表示“不等于”
有方向研究假设
有方向研究假设(directional research hypothesis)反映群体间的差异,而且差异的方向是确定的。可以用下面的式子表示:$$H_i:\overline{X}\_9 < \overline{X}\_{12}$$ 其中
- Hi 表示第一个(可能有几个)研究假设的符号
- $\overline{X}\_9$ 表示 12 年级学生样本的平均记忆成绩
- $\overline{X}\_{12}$ 表示 9 年级学生样本的平均记忆成绩
- < 表示“小于”
概率和概率的重要性
正态曲线(或钟形曲线)
正态曲线(normal curve,叫做钟型曲线,或钟形曲线)就是具备三个特征的数据分布的形象表示。下图表明了这三个特征。
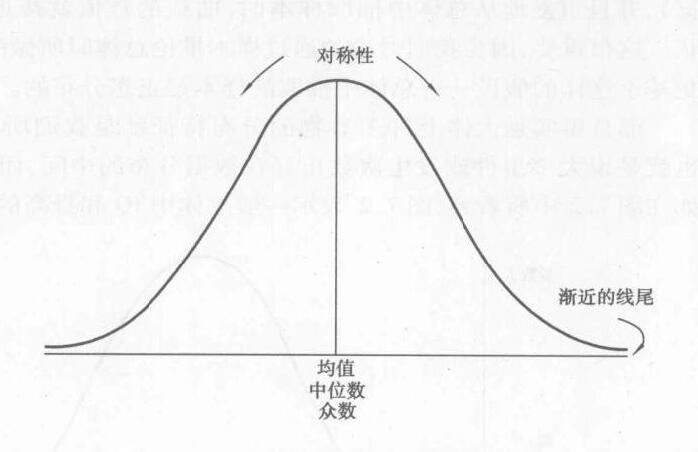
正态曲线表示均值、中位数和众数相等的数值分布。正态曲线没有偏度。正态曲线有一个很好的波峰(只有一个),而且波峰正好处于中间。
正态曲线以均值为中心完全对称。曲线的一半是另一半的镜像。正态曲线的双尾是渐进的(asymptotic)。含义是曲线的双尾越来越逼近横轴,但是永远不会与横轴相交。
z 值
z 值就是原始数据与数据分布均值的差除以标准差所得的结果。其公式为:$$z = \frac{(X - \overline{X})}{s}$$ 其中
- z 是z 值
- X 是具体的数值
- $\overline{X}$ 是数据分布的数值
- s 是数据分布的标准差
两个群体的t检验
计算检验统计量
以下公式是计算独立均值t检验中t值的公式。公式的分子是均值之间的差。群体内和群体间的变化的数量构成分母。 $$t = \frac{\overline{X_1} - \overline{X_2}}{\sqrt{\left[ \frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2-2} \right]\left[ \frac{n_1 + n_2}{n_1n_2} \right]}}$$ 其中
- $\overline{X_1}$ 表示群体 1 的均值
- $\overline{X_2}$ 表示群体 2 的均值
- n1 表示群体 1 中参与者的数量
- n2 表示群体 2 中参与者的数量
- s12 表示群体 1 的方差
- s22 表示群体 2 的方差
计算和理解效应量
最简单的计算效应量(effect size)的方式就是以均值之间的差除以任何一个群体的标准差。这样做有一定的风险——因为假定两个群体的标准差(和方差)相等。 $$ES = \frac{\overline{X_1} - \overline{X_2}}{SD}$$ 其中
- ES 表示效应量
- $\overline{x_1}$ 表示群体 1 的均值
- $\overline{x_2}$ 表示群体 2 的均值
- SD 表示任何一个群体的标准差
两个相关群体的均值检验
非独立样本t检验介绍
为什么用非独立均值检验?非独立均值检验表明是相同的群体在两种不同的条件下进行相同的研究。非独立均值t检验包含每一群体均值的比较,而且重点是不同数值之间的差异。如下公式,两次测试的差异总和构成分子,表示群体之间的差异。 $$t = \frac{\sum{D}}{\sqrt{\frac{n\sum{D^2} - (\sum{D})^2}{n-1}}}$$ 其中
- ∑D 表示群体间差异的总和
- ∑D2 表示群体间差异的平方和
- n 表示成对观察的参与者数量
t 检验统计量的计算步骤:
- 零假设和研究假设的表述。
- 设置零假设的风险水平(或显著性水平,或第一类错误)。
- 选择合适的检验统计量。
- 计算检验统计值(也叫做实际值)。
- 使用特定统计量的临界值分布表确定拒绝零假设需要的值。
- 比较实际值和临界值。
- 和 8. 做出决定。如果实际值大于临界值就不能接受零假设。如果实际值没有超过临界值,零假设就是最有力的解释。
尝试进行方差分析
方差分析的不同类型
方差分析有许多不同的形式。最简单的形式是简单方差分析(simple analysis of variance),只分析一个因素或者一个处理变量,而有两个以上的群体受到这个因素的影响。简单方差分析也叫做一元方差分析(one-way analysis of variance),因为只有一个分组维度。
实际上,方差分析在许多情况下类似于t检验。在这两项检验中都需要计算均值之间的差异。但方差分析要处理两个以上的均值。
更复杂的方差分析类型是析因设计(factorial design),是分析一个以上的处理变量。
计算检验统计量
简单方差分析检验两个以上的群体在一个因素或一个维度上的均值差异。
任何分析如果:
- 只有一个维度或者一个处理变量
- 分组因素有两个以上的层级,而且
- 关注不同群体在平均成绩上的差异
就需要使用简单方差分析。
F 值是检验假设也就是群体之间有差异的检验统计量,计算公式如下。 $$F = \frac{MS\_{between}}{MS\_{within}}$$
方差分析公式(是一个比率)比较组间的变化量(由于分组因素产生)与组内的变化量(由于随机因素产生)。如果比值为 1,那么组内差异产生的变化量等于组间差异产生的变化量,而且组间的任何差异都不显著。如果组间差异的平均值变大(也就是比率的分子变大),F 值也变大。如果F 值变大,在所有的F 值分布中就会更趋向于极值,也就是更可能由于随机因素之外的因素影响。
F 检验统计量的计算步骤:
- 零假设和研究假设的表述。
- 设置零假设的风险水平(或显著性水平、或第一类错误)。风险水平完全由研究者决定。
- 选择合适的检验统计量。
- 计算检验统计值(也叫做实际值)。
- 使用特定统计量的临界值分布表确定拒绝零假设需要的值。
- 比较实际值和临界值。
- 和 8.做出决定。如果实际值大于临界值就不能接受零假设。如果实际值没有超过临界值,零假设就是最有力的解释。
使用线性回归
什么是估计
估计的基本含义就是使用已经收集的数据集(如变量X、Y的数据),计算变量如何相关,接着使用相关系数以及X的信息来估计Y。
相关系数的绝对值越大,依据相关以一个变量估计另一个变量的准确性越高,因为这两个变量共享的部分越多,依据第一个变量的了解就可以更多地了解第二个变量。
估计的逻辑
估计是以过去的结果估计未来结果的活动。当我们想通过一个变量估计另一个变量,我们首先需要计算两个变量之间的相关系数。
通过建立回归等式(regression equation),并使用这个等式建立回归线(regression line)。回归线反映我们以变量X的值估计变量Y值的最好猜测。
回归线也叫做最优拟合线(line of best fit)。回归线最好地拟合了数据,因为这条线将每个数据点与回归线的距离最小化。
每一个具体数据点和回归线的距离就是估计误差(error in prediction)——是两个变量之间相关的直接反映。
如果是完全相关,所有的数据点将沿着 45° 角成为一条直线,而且回归线通过每一个数据点、
绘制拟合数据的最优直线
理解估计的最简单的方式就是依据一个变量值(我们成为X——独立变量,independent variable 或估计变量,predictor)确定另一个变量的值(我们成为Y——依赖变量,dependent variable 或标准变量,criterion)。 以下公式是回归线的一般公式,这个公式在高中或者大学的数学课程中都可能用到,对你来说应该很熟悉。这个公式与其他任何直线公式一样。 Y′ = bX + a 其中
- Y′ 表示已知X值的Y的估计值。
- b 表示直线的斜率或者方向。
- a 表示直线与y 轴相交的点。
- X 表示用于估计的数值。
以下公式用于计算回归线的斜率(直线公式中的 b): $$b = \frac{\sum{XY} - (\sum{X}\sum{Y})/n}{\sum{X^2}-[(\sum{X})^2/n]}$$
以下公式用于计算直线与y轴相交的点(直线公式中的a): $$a = \frac{\sum{Y}-b\sum{X}}{n}$$
多元回归(multiple regression)
多元回归的模型是: Y′ = bX1 + bX2 + a 其中 X1 表示第一个独立变量的数值 X2 表示第二个独立变量的数值 b 表示特定变量的回归权重
使用多元估计变量应遵守的重要守则
如果要使用不止一个估计变量,要谨记遵守下面的两项重要的原则:
- 如果选择一个独立变量估计一个结果,要选择与被估计变量(Y)相关的估计变量(X)。也就是这两个变量有共变的部分(记住,它们应该相关)。
- 如果选择不止一个独立变量或估计变量(如X1与X2),要尽量选择相互独立或者不相关的变量,但是都要与结果变量或被估计变量(Y)相关。
卡方和其他非参数检验
单样本卡方检验介绍
单样本卡方检验的原理是,就任何事件的发生而言都可以很容易地计算随机预期的结果。
计算卡方检验统计量
卡方检验要进行观察值和随机预期值的比较。下列公式就是单样本卡方检验的卡方值计算公式。 $$X^2 = \sum{\frac{(O - E)^2}{E}}$$ 其中
- X2 表示卡方值
- ∑ 是连加符号
- O 表示观察频数
- E 表示预期频数
理解信度和效度
1. 定类测量水平 定类测量水平(nominal level of measurement)是以观察结果的属性特征定义,也就是观察结果只适合一个而且唯一的一个分类或层级。例如,性别是定类变量(男性和女性)。定类测量水平的各个类别相互排斥,例如,性别不能同时是男性和女性。
2. 定序测量水平 定序测量水平(ordinal level of measurement)的“序”表示次序,而且被测量的事物按照它们的属性特征排序。最好的案例是一份工作的应征者的次序。
3. 定距测量水平 定距测量水平(interval level of measurement),是指检验或评估工具是基于某种连续体。例如,你的词汇测试成绩是 10 个单词正确,是 5 个单词正确的两倍。
4. 定比例测量水平 定比测量水平(ration level of measurement)的评估工具的特征是测量尺度中绝对零值的存在。这意味着没有要测量的任何特征。
信度
信度就是一个测试或者你使用的其他任何测量工具对事物的测量可以保持一致性。
信度的不同类型
信度有几种不同的类型,现在主要介绍最重要也是最常用的四种类型。

1. 再测信度(前测-后测信度) 再测信度(test-retest reliability)用于检验一个测试在不同时期是否可信。
例如,你想建立检验不同类型职业项目的选择偏好的测试。你在六月份进行了测试,接着在九月份进行了相同的测试(保持相同很重要)。那么你计算两次测试的得分集(记住是相同的人进行了两次测试)是否相关,也就是进行了信度的测试。再测信度是检验不同时间的变化或差异所必需的信度。
你必须确保你测量的内容是以可信的方式测量的,这样你得到的测试结果才能与每个个体每个时间的值更接近。
2. 平行形式信度 平行形式信度(parallel forms reliability)用于检验相同测试的不同形式的等价性和相似性。
3. 内在一致性信度 内在一致性信度(internal consistency reliability)用于确定测试中的项目是否彼此一致,都只表示一个维度、一个结构或一个关注的领域。 计算克隆巴赫系数的公式: $$\delta = (\frac{k}{k-1})(\frac{s_y^2-\sum{s_i^2}}{s_y^2})$$ 其中
- k 表示项目的个数
- sy2 表示观察值的方差
- ∑sy2 表示每一个项目的方差的总和
4. 评分者信度 评分者信度(interrater reliability)是两个评分者对观察结果判断的一致程度的测量。 评分者信度可以使用下面的简单公式计算: $$评分者之间的信度 = \frac{一致的数量}{可能一致的数量}$$
效度
效度(validity),就是表示工具能够测量要测量的内容的性质。有效的测试是测量应该测量的内容。
效度的不同类型
效度有不同的类型,我们介绍最重要也是最常用的三种类型。

内容效度
内容效度(content validity)就是测试项目能代表设计测试要测量的总体项目的性质。内容效度常用于成绩测试(例如从一年级的拼写测试到学术能力测试的任何测试)。
建立内容效度。建立内容效度实际上非常容易。所有你需要做的就是确定你的地方合作专家。
准则效度
准则效度(criterion validity)是评价测试是否反映现在和未来的一组能力。如果准则是发生在现在,我们就讨论同步效度(concurrent criterion validity)。如果准则是发生在未来,我们就讨论预测效度(predictive concurrent validity)。对于准则效度的应用,不需要同时建立同步效度和预测效度,按照测试目的的需要选择适用的那个就行了。
建构效度
建构效度(construct validity)是最有趣也是最难建立的效度,因为建构效度是基于测试或测量工具背后的基本的结构或概念的。
完!